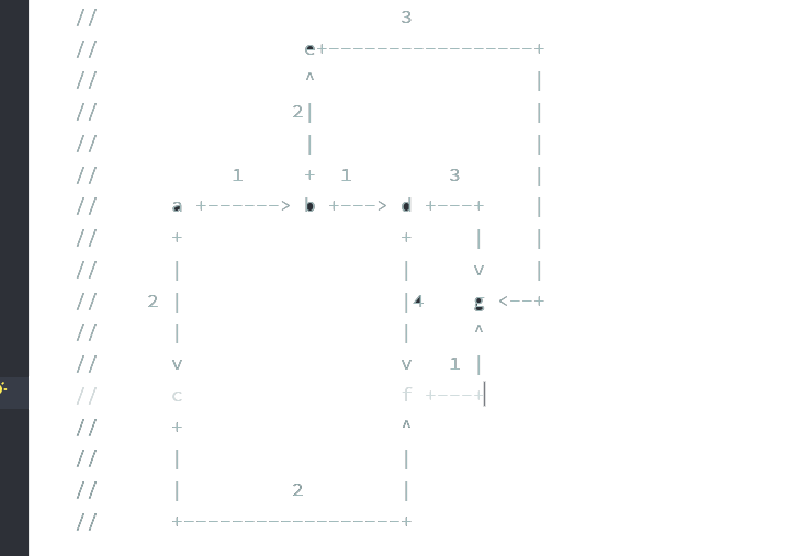假设有如下一个图
// 3
// e+-----------------+
// ^ |
// 2| |
// | |
// 1 + 1 3 |
// a +------> b +---> d +---+ |
// + + | |
// | | v |
// 2 | |4 g <--+
// | | ^
// v v 1 |
// c f +---+
// + ^
// | |
// | 2 |
// +------------------+
我们要做的是找到点a到点g的最小距离,并且点与点之间会有权值,这时候我们可以使用迪杰斯特拉算法
使用这个算法,路径是这样的.
首先先把上图转化成邻接矩阵.
array(
'a' => array('a' => INF, 'b' => 1, 'c' => 2, 'd' => INF, 'e' => INF, 'f' => INF, 'g' => INF),
'b' => array('a' => INF, 'b' => INF, 'c' => INF, 'd' => 1, 'e' => 2, 'f' => INF, 'g' => INF),
'c' => array('a' => INF, 'b' => INF, 'c' => INF, 'd' => INF, 'e' => INF, 'f' => 2, 'g' => INF),
'd' => array('a' => INF, 'b' => INF, 'c' => INF, 'd' => INF, 'e' => INF, 'f' => 4, 'g' => 3),
'e' => array('a' => INF, 'b' => INF, 'c' => INF, 'd' => INF, 'e' => INF, 'f' => INF, 'g' => 3),
'f' => array('a' => INF, 'b' => INF, 'c' => INF, 'd' => INF, 'e' => INF, 'f' => INF, 'g' => 1),
'g' => array('a' => INF, 'b' => INF, 'c' => INF, 'd' => INF, 'e' => INF, 'f' => INF, 'g' => INF),
);
- 初始化一个关闭列表数组,代表已经寻找过的,(防止回溯), 里面放入开始节点,因为第一个寻找的就是开始节点
- 需要一个开放列表数组,存储所有已经找过的最短路径,里面初始化好
a到各点的距离(INF是无效大,代表这个点无法到达,也可以用一个很大权值代表)
closeList(1) {
a => true
}
openList(7) {
a => INF
b => 1
c => 2
d => INF
e => INF
f => INF
g => INF
}
- 循环邻接矩阵的第一行,拿到开放列表中最小值
1,索引为b`,并把这个索引标记到关闭列表. - 得到上一行最小值的索引,取邻接矩阵的这一行数据,就是第
b行的数据. - 然后这一行的每一个数据加上取得的最小值,看是否小于开放列表的数据.(如,第
b行的a是INF+ 最小值1并不小于开放列表的a => INF)(如,第b行的d是1+ 最小值1等于2小于开放列表的d => INF,则这时候把开放列表中的d从原来的INF改为2)经过此次循环,数据将变成这样子.
closeList(1) {
a => true,
b => true
}
openList(7) {
a => INF
b => 1
c => 2
d => 2
e => 3
f => INF
g => INF
}
- 重复上一个步骤
- 循环邻接矩阵的第一行,拿到开放列表中最小值
2,索引为c(因为b`已经被标记在关闭列表了),并把这个索引标记到关闭列表. - 得到上一行最小值的索引,取邻接矩阵的这一行数据,就是第
c行的数据. - 然后这一行的每一个数据加上取得的最小值,看是否小于开放列表的数据.(第
c行只有一个f => 2加上最小值2等于4小于开放列表中的f => INF)经过此次循环,数据将变成这样子.
closeList(1) {
a => true,
b => true,
c => true
}
openList(7) {
a => (NF
b => 1
c => 2
d => 2
e => 3
f => 4
g => INF
}
- 重复上一个步骤
- 循环邻接矩阵的第一行,拿到开放列表中最小值
2,索引为d(因为b和c`已经被标记在关闭列表了),并把这个索引标记到关闭列表. - 得到上一行最小值的索引,取邻接矩阵的这一行数据,就是第
d行的数据. - 然后这一行的每一个数据加上取得的最小值,看是否小于开放列表的数据.(第
d行f => 4加上最小值2等于6并不小于开放列表中的f => 4,所以舍弃这跳路径)经过此次循环,数据将变成这样子.
closeList(1) {
a => true,
b => true,
c => true
}
openList(7) {
a => (NF
b => 1
c => 2
d => 2
e => 3
f => 4
g => 5
}
- 以此类推,直至循环结束后,开放列表里存储的是任意一个点到
a的最短权值距离.
openList(7) {
a => INF
b => 1
c => 2
d => 2
e => 3
f => 4
g => 5
}
实现代码如下:
<?php
class Dijkstra
{
protected $matrix;
public function __construct()
{
//有向图存储
$this->matrix = array(
'a' => array('a' => INF, 'b' => 1, 'c' => 2, 'd' => INF, 'e' => INF, 'f' => INF, 'g' => INF),
'b' => array('a' => INF, 'b' => INF, 'c' => INF, 'd' => 1, 'e' => 2, 'f' => INF, 'g' => INF),
'c' => array('a' => INF, 'b' => INF, 'c' => INF, 'd' => INF, 'e' => INF, 'f' => 2, 'g' => INF),
'd' => array('a' => INF, 'b' => INF, 'c' => INF, 'd' => INF, 'e' => INF, 'f' => 4, 'g' => 3),
'e' => array('a' => INF, 'b' => INF, 'c' => INF, 'd' => INF, 'e' => INF, 'f' => INF, 'g' => 3),
'f' => array('a' => INF, 'b' => INF, 'c' => INF, 'd' => INF, 'e' => INF, 'f' => INF, 'g' => 1),
'g' => array('a' => INF, 'b' => INF, 'c' => INF, 'd' => INF, 'e' => INF, 'f' => INF, 'g' => INF),
);
}
public function search()
{
$start = 'a';
$end = 'g';
// 存储路径上节点距离源点的最小距离
$closeList = [$start => true];
$openList = array();
// 初始化图中节点与源点的最小距离
foreach ($this->matrix[$start] as $key => $value) {
// 得到各个点到源点的距离
$openList[$key] = $value;
}
foreach ($this->matrix as $y => $item) {
// 设置为初始索引,即使找不到最小值,也不会影响
$minIndex = $start;
$minVal = INF;
// 找到当前行中最小的值,并选取作为优选
foreach ($item as $x => $val) {
// 如果此节点已经寻找过(防止回溯)
// 如果没有找到最短路径, 并且最短距离数据的当前值更小
// 每一次都从源点距离数据数组中取最小的出来,并且必须是还未访问过的
if (! array_key_exists($x, $closeList) && $openList[$x] < $minVal) {
$minVal = $openList[$x];
$minIndex = $x;
}
}
// 标记这个节点已经找过, 不能再倒回去找
$closeList[$minIndex] = true;
// 当找到最小轴之后,再去循环最小轴的那一行数据,
// 从那一行中拿出每一个数据加上最小值和节点距离源点数组作比较
foreach ($this->matrix[$minIndex] as $k => $v) {
// 如果当前的这个点值加上当前轴往外扩展的距离如果更小
if (! array_key_exists($k, $closeList) && ($minVal+$v < $openList[$k])) {
$openList[$k] = $minVal+$v;
}
}
}
var_dump($openList[$end]);
}
}