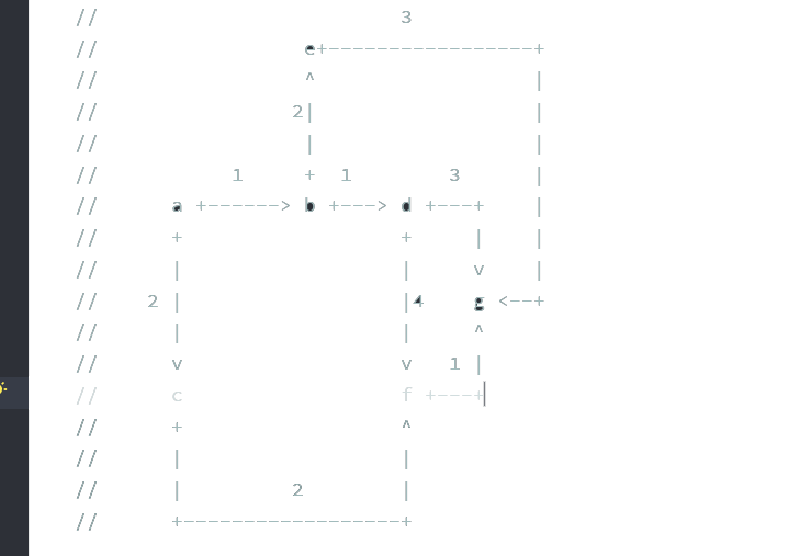Dijkstra Algorithm

Suppose we have the following graph:

        //                         3
        //                 e+-----------------+
        //                 ^                  |
        //                2|                  |
        //                 |                  |
        //           1     +  1        3      |
        //      a +------> b +---> d +---+    |
        //      +                  +     |    |
        //      |                  |     v    |
        //    2 |                  |4    g <--+
        //      |                  |     ^
        //      v                  v   1 |
        //      c                  f +---+
        //      +                  ^
        //      |                  |
        //      |         2        |
        //      +------------------+

To find the shortest path from node a to node g, we can use the Dijkstra algorithm. Here’s how it works:

Convert the graph to an adjacency matrix:

array(
    'a' => array('a' => INF, 'b' => 1,   'c' => 2,   'd' => INF, 'e' => INF, 'f' => INF, 'g' => INF),
    'b' => array('a' => INF, 'b' => INF, 'c' => INF, 'd' => 1,   'e' => 2,   'f' => INF, 'g' => INF),
    'c' => array('a' => INF, 'b' => INF, 'c' => INF, 'd' => INF, 'e' => INF, 'f' => 2,   'g' => INF),
    'd' => array('a' => INF, 'b' => INF, 'c' => INF, 'd' => INF, 'e' => INF, 'f' => 4,   'g' => 3),
    'e' => array('a' => INF, 'b' => INF, 'c' => INF, 'd' => INF, 'e' => INF, 'f' => INF, 'g' => 3),
    'f' => array('a' => INF, 'b' => INF, 'c' => INF, 'd' => INF, 'e' => INF, 'f' => INF, 'g' => 1),
    'g' => array('a' => INF, 'b' => INF, 'c' => INF, 'd' => INF, 'e' => INF, 'f' => INF, 'g' => INF),
);

Initialize data structures:

closedList: Tracks visited nodes (start with a)
openList: Stores minimum distances from start node

closedList(1) {
    a => true
}

openList(7) {
    a => INF
    b => 1
    c => 2
    d => INF
    e => INF
    f => INF
    g => INF
}

Iteration process:

Find node with minimum distance in openList that’s not in closedList
Update distances for adjacent nodes
Mark node as visited in closedList

First iteration:

closedList(2) {
    a => true,
    b => true
}

openList(7) {
    d => 2    // b->d (1+1)
    e => 3    // b->e (1+2)
    ...other values remain...
}

Final result:

openList(7) {
    a => INF
    b => 1
    c => 2
    d => 2
    e => 3
    f => 4    // c->f (2+2)
    g => 5    // d->g (2+3)
}

The shortest path from a to g is 5 through path a->b->d->g.

Implementation code:

<?php

class Dijkstra
{
    protected $matrix;

    public function __construct()
    {
        // Directed graph representation
        $this->matrix = array(
            'a' => array('a' => INF, 'b' => 1,   'c' => 2,   'd' => INF, 'e' => INF, 'f' => INF, 'g' => INF),
            'b' => array('a' => INF, 'b' => INF, 'c' => INF, 'd' => 1,   'e' => 2,   'f' => INF, 'g' => INF),
            'c' => array('a' => INF, 'b' => INF, 'c' => INF, 'd' => INF, 'e' => INF, 'f' => 2,   'g' => INF),
            'd' => array('a' => INF, 'b' => INF, 'c' => INF, 'd' => INF, 'e' => INF, 'f' => 4,   'g' => 3),
            'e' => array('a' => INF, 'b' => INF, 'c' => INF, 'd' => INF, 'e' => INF, 'f' => INF, 'g' => 3),
            'f' => array('a' => INF, 'b' => INF, 'c' => INF, 'd' => INF, 'e' => INF, 'f' => INF, 'g' => 1),
            'g' => array('a' => INF, 'b' => INF, 'c' => INF, 'd' => INF, 'e' => INF, 'f' => INF, 'g' => INF),
        );
    }

    public function search()
    {
        $start = 'a';
        $end = 'g';

        // Track visited nodes
        $closeList = [$start => true];
        // Store minimum distances
        $openList = $this->matrix[$start];

        foreach ($this->matrix as $y => $item) {
            $minIndex = $start;
            $minVal = INF;

            // Find minimum unvisited node
            foreach ($item as $x => $val) {
                if (!isset($closeList[$x]) && $openList[$x] < $minVal) {
                    $minVal = $openList[$x];
                    $minIndex = $x;
                }
            }

            $closeList[$minIndex] = true;

            // Update distances
            foreach ($this->matrix[$minIndex] as $k => $v) {
                if (!isset($closeList[$k]) && ($minVal + $v < $openList[$k])) {
                    $openList[$k] = $minVal + $v;
                }
            }
        }

        echo "Shortest distance: " . $openList[$end];
    }
}